Memory Trigger

1. Larget Infinity
2. Ordinal number concept

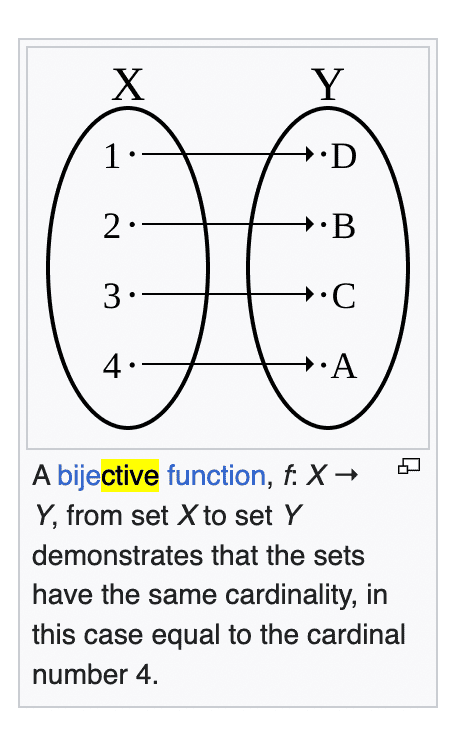
Cardinal numbers

Cardinal number

• https://en.wikipedia.org/wiki/Cardinal_number
• Cardinal numbers are a group of object, where their order (greater or equal to) and arithmetic are all defined by operations of the seat each of them represent

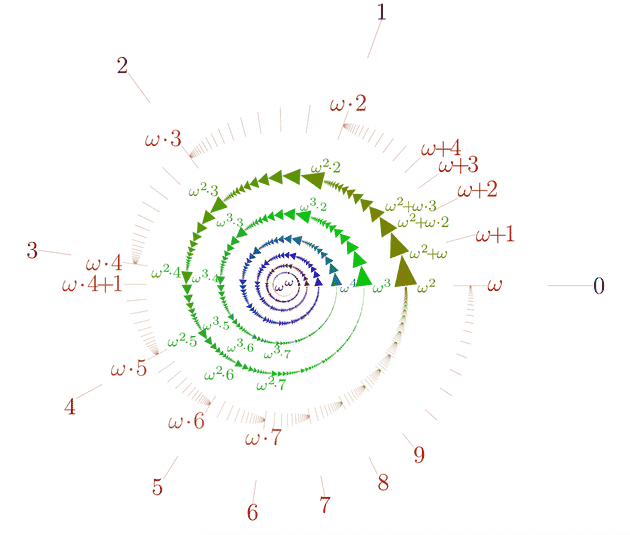
Ordinal numbers

Axiom of choice

Definition

• Informally put, the axiom of choice says that given any collection of sets, each containing at least one element, it is possible to construct a new set by choosing one element from each set, even if the collection is infinite
• Included in the Zermelo-Fraenkel axioms
• With this axiom we can prove the Banach Tarski paradox
• https://www.youtube.com/shorts/e28mB2DU_ZI

Cantor's theorem

• Consequently, the theorem implies that there is no largest cardinal number (colloquially, "there's no largest infinity")

Cantor's diagonal argument

Proof that the real numbers are uncountable